Навигация
Движение переводит плоскость в плоскость
4. Движение переводит плоскость в плоскость.
Докажем это свойство. Пусть a - произвольная плоскость. Отметим на ней любые три точки A, B, C, не лежащие на одной прямой. Проведем через них плоскость a'.
Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a'.
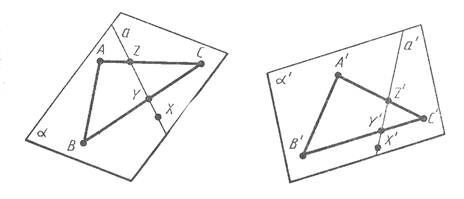 Пусть X - произвольная точка плоскости a. проведем через нее какую-нибудь прямую a в плоскости a, пересекающую треугольник ABXC в двух точках Y и Z. Прямая а перейдет при движении в некоторую прямую a'. Точки Y и Z прямой a перейдут в точки Y' и Z', принадлежащие треугольнику A'B'C', а значит, плоскости a'.
Пусть X - произвольная точка плоскости a. проведем через нее какую-нибудь прямую a в плоскости a, пересекающую треугольник ABXC в двух точках Y и Z. Прямая а перейдет при движении в некоторую прямую a'. Точки Y и Z прямой a перейдут в точки Y' и Z', принадлежащие треугольнику A'B'C', а значит, плоскости a'.
Итак прямая a' лежит в плоскости a'. Точка X при движении переходит в точку X' прямой a', а значит, и плоскости a', что и требовалось доказать.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
III. Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.
Симметрия относительно точки
 Пусть О - фиксированная точка и X - произвольная точка плоскости. Отложим на продолжении отрезка OX за точку O отрезок OX', равный OX. Точка X' называется симметричной точке X относительно точки O. Точка, симметричная точке O, есть сама точка O. Очевидно, что точка, симметричная точке X', есть точка X.
Пусть О - фиксированная точка и X - произвольная точка плоскости. Отложим на продолжении отрезка OX за точку O отрезок OX', равный OX. Точка X' называется симметричной точке X относительно точки O. Точка, симметричная точке O, есть сама точка O. Очевидно, что точка, симметричная точке X', есть точка X.
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точке O, называется преобразованием симметрии относительно точки O. При этом фигуры F и F' называются симметричными относительно точки O.
 Если преобразование симметрии относительно точки O переводит фигуру F в себя, то она называется центрально-симметричной, а точка O называется центром симметрии.
Если преобразование симметрии относительно точки O переводит фигуру F в себя, то она называется центрально-симметричной, а точка O называется центром симметрии.
Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей.
Теорема: Преобразование симметрии относительно точки является движением.
Доказательство. Пусть X и Y - две произвольные точки фигуры F. Преобразование симметрии относительно точки O переводит их в точки X' и Y'. Рассмотрим треугольники XOY и X'OY'. Эти треугольники равны по первому признаку равенства треугольника. У них углы при вершине O равны как вертикальные, а OX=OX', OY=OY' по определению симметрии относительно точки O. Из равенства треугольников следует равенство сторон: XY=X'Y'. А значит, что симметрия относительно точки O есть движение. Теорема доказана.
Симметрия относительно прямой
Пусть g - фиксированная прямая. Возьмем произвольную точку X и опустим перпендикуляр AX н прямую g. На продолжении перпендикуляра за точку A отложим отрезок AX', равный отрезку AX. Точка X' называется симметричной точке X относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке X', есть точка X.
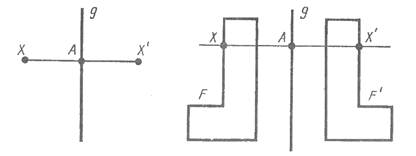 Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g.
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g.
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.
Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, является осями симметрии прямоугольника. Прямые на которых лежат диагонали ромба, является его осями симметрии.
Теорема: Преобразование симметрии относительно прямой является движением.
 Доказательство. Примем данную прямую за ось у декартовой системы координат. Пусть произвольная точка A (x;y) фигуры F переходит в точку A' (x';y') фигуры F'. Из определения симметрии относительно прямой следует, что у точек A и A' равные ординаты, а абсциссы отличаются только знаком: x' = -x.
Доказательство. Примем данную прямую за ось у декартовой системы координат. Пусть произвольная точка A (x;y) фигуры F переходит в точку A' (x';y') фигуры F'. Из определения симметрии относительно прямой следует, что у точек A и A' равные ординаты, а абсциссы отличаются только знаком: x' = -x.
Возьмем две произвольные точки A (x;y) и B (x;y). Они перейдут в точки A' (-x;y) и B' (-x;y).
Имеем:
AB2=(x2-x1)2+(y2-y1)2
A'B'2=(-x2+ x1) 2+(y2-y1)2
Отсюда видно, что AB=A'B'. А значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.
Симметрия относительно плоскости
Пусть a - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость a и на его продолжении за точку Aоткладываем отрезок AX', равный XA. Точка X' называется симметричной точке X относительно плоскости a, а преобразование, которое переводит X в симметричную ей точку X', называется преобразованием симметрии относительно плоскости a.
Если точка X лежит в плоскости a, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости a переводит фигуру в себя, то фигура называется симметричной относительно плоскости a, а плоскость a называется плоскостью симметрии этой фигуры.
Поворот
 Поворот плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из точки, поворачивается на один и тот же угол в одном и том же направлении.
Поворот плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из точки, поворачивается на один и тот же угол в одном и том же направлении.
Это значит, что если при поворот около точки O точка переходит в точку X', то лучи OX и OX' образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота. Преобразование фигур при повороте плоскости также называется поворотом.
Параллельный перенос в пространстве
Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a,b,c одни и те же для всех точек (x; y; z). Параллельный переносов пространстве задается формулами
x'=x+a, y'=y+b, z'=z+c,
выражающими координаты x', y', z' точки, в которую переходит точка (x; y; z) при параллельном переносе. Так же, как и на плоскости, доказываются следующие свойства параллельного переноса:
1. Параллельные перенос есть движение.
2. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'.
Новым для параллельного переноса в пространстве является следующее свойство:
5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную её плоскость.

Действительно, пусть a - произвольная плоскость, проведем в этой плоскости две пересекающиеся прямые a и b. При параллельном переносе прямые a и b переходят либо в себя, либо в параллельные прямые a' и b'. Плоскость a переходит в некоторую плоскость a', проходящую через прямые a' и b'. Если плоскость a' не совпадает с a, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, она параллельна a, что и требовалось доказать.
Список использованной литературы:
1. Учебник Геометрии 7-11 классы. А.В. Погорелов
2. Учебник Геометрии 10-11 классы. А.Д. Александров.
Похожие работы
... С2. Треугольники А2ВС2 и А1В1С1 равны по третьему признаку. Из равенства треугольников следует равенство углов А2ВС2 и А1В1С1. Значит, углы ABC и А1В1С1 равны, что и требовалось доказать. 3. ПОДОБИЕ ФИГУР Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Для обозначения подобия фигур используется специальный значок: ∞. Запись F∞F' читается ...
... - медианы треугольников; 4. , , где BH и B1H1 высоты треугольников. §5. Опытная работа Цель опытной работы: выявление методических особенностей изучения темы «Подобные треугольники» в средней школе. Идея: для выявления методических особенностей необходимо провести несколько уроков по разработанной методики, в конце обучения провести контрольную работу, при анализе которой можно судить о ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... различия между испытуемыми контрольной и экспериментальной групп послужили основанием для проведения целенаправленной педагогической работы по развитию представлений детей экспериментальной группы о форме предметов. 2.2 Использование задач-головоломок в развитие представлений о форме предметов у детей экспериментальной группы Представления детей о форме предметов имеет большое значение при ...




0 комментариев